Corpo Nero

Cos'è un corpo nero? Il corpo nero è soltanto un oggetto ideale, e lo si chiama così perché assorbe molto bene tutta la radiazione che ci cade sopra. Un'ottima approssimazione di corpo nero è un contenitore in cui sia stato fatto un piccolo foro: a temperatura ambiente il foro appare assolutamente nero, ed il motivo è che la radiazione luminosa che entra nel contenitore viene Edoardo Milotti - Laboratorio di Fisica I, A. A. 2007-2008 diffusa molte volte al suo interno, ed è molto più probabile che alla fine venga assobita piuttosto che riesca ad uscire dallo stesso foro da cui è entrata. 

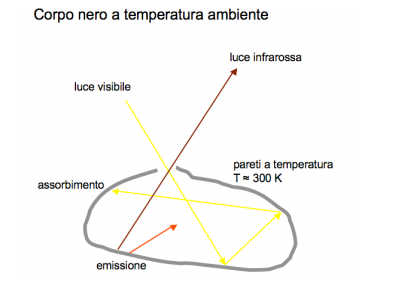
In questo modo la radiazione che entra nella cavità scalda le pareti, che riemettono radiazione infrarossa. Quando viene raggiunto l'equilibrio termodinamico l'energia elettromagnetica che entra nella cavità è uguale a quella irraggiata dal foro, ma il tipo di radiazione emesso dipende dalla temperatura della cavità. Da questo punto di vista si capisce allora che un corpo nero non è veramente nero: un oggetto come quello descritto sopra ci appare nero a temperatura ambiente perché assorbe radiazione visibile, la radiazione visibile viene convertita in radiazione nel dominio delle microonde o nell'infrarosso lontano in seguito all'assorbimento e riemissione da parte delle pareti (che nel nostro caso sono a temperatura ambiente), e noi non siamo in grado di vedere la radiazione che esce dal foro. Se le pareti del corpo nero fossero a temperatura elevata, diciamo intorno a 1000 °C, allora il foro riemetterebbe radiazione visibile, e il corpo non sarebbe affatto nero. 

_{L'emissione infrarossa degli oggetti a temperatura ambiente può venire visualizzata per mezzo di telecamere sensibili all'infrarosso. Le immagini risultanti (termografie) sono spesso interessanti: in questo caso si vede che il sacco nero è in realtà trasparente all'infrarosso, mentre gli occhiali che sono trasparenti per la luce visibile, sono opachi nell'infrarosso (dal sito http://coolcosmos.ipac.caltech.edu/cosmic_kids/learn_ir/index. html)}

A questo punto siamo arrivati all'idea fondamentale: un corpo nero è oggetto in cui la materia che assorbe ed emette la radiazione è in equilibrio termico con la radiazione stessa. Se una parte della radiazione può sfuggire dal corpo nero, allora l'equilibrio si mantiene solo se viene fornita tanta energia quanta ne sfugge per irraggiamento. Cerchiamo ora di capire come funziona questo equilibrio termico studiando una cavità particolarmente semplice, una cavità unidimensionale con delle pareti metalliche, che rappresenta ovviamente un'astrazione, ma che ci servirà per cominciare. 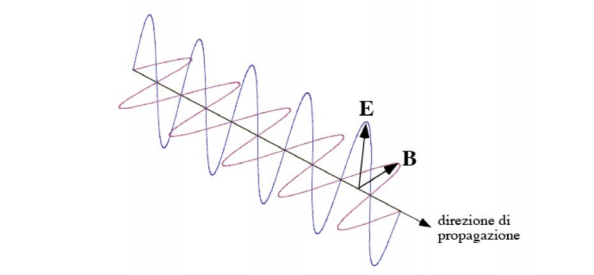Ricordiamo anzitutto che le onde elettromagnetiche sono onde trasversali: l'oscillazione del campo elettrico (e magnetico) dell'onda è perpendicolare alla direzione di propagazione.

La cavità seleziona le onde elettromagnetiche: all'equilibrio, nella cavità non ci possono essere onde elettromagnetiche arbitrarie, ma solo quelle che hanno campo elettrico nullo sulle pareti della cavità (se supponiamo che le pareti siano dei conduttori perfetti, allora il campo elettrico tangenziale deve essere nullo). Ciò significa che la cavità può contenere solo un numero intero di mezze lunghezze d'onda, così che se L è la lunghezza della cavità, allora il campo stazionario contenuto nella cavità deve avere una lunghezza d'onda λ  tale che L = nλ / 2 dove n è un intero, e quindi le frequenze permesse del campo elettrico sono date da  \( v= n c \div (2 L) = n v_{0}  \) e analogamente \( n= 2 L \div (c v) \)

Per il teorema di equipartizione dell'energia, ciascun termine quadratico della funzione energia del sistema fisico dà un contributo kT/2 all'energia media, e quindi, ricordando che la funzione energia di un oscillatore è la somma di due termini quadratici (energia cinetica e potenziale) e sommando anche sui due stati di polarizzazione, l'energia associata a ciascun modo di oscillazione elettromagnetico è 2kT, per cui l'energia totale della radiazione in equilibrio termico con le pareti è infinita! Ma questo è impossibile, in questo modo non potrebbe mai esserci equilibrio termico, perché la cavità sarebbe in grado di assorbire infinita energia ad una data temperatura, mentre invece noi siamo in grado di realizzare sperimentalmente delle cavità in equilibrio termico con la radiazione. Otteniamo lo stesso risultato anche nell'approssimazione continua, vale a dire supponendo che n sia abbastanza grande da poterlo trattare come una variabile continua.

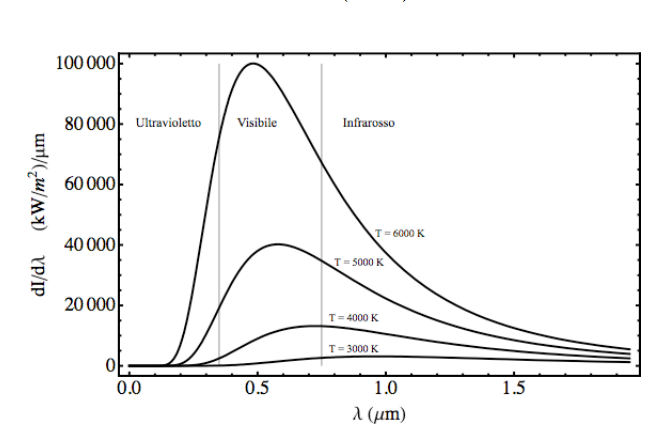
La densità spettrale di energia diverge per alte frequenze: questa è la cosiddetta catastrofe ultravioletta (la divergenza avviene all'estremità dello spettro corrispondente alle frequenze dell'ultravioletto e più alte). Sperimentalmente si trova che il comportamento della densità spettrale è ben diverso: non c'è alcuna catastrofe ultravioletta, mentre invece lo spettro raggiunge un massimo e poi declina alle alte frequenze. Come si può risolvere questo problema? Torniamo ora ad una delle ipotesi fondamentali che abbiamo fatto all'inizio, e cioè che ogni grado di libertà possedesse un'energia media data dal teorema di equipartizione che suppone che l'energia sia una variabile continua, e noi abbiamo valutato appunto degli integrali. Ma supponiamo che non lo sia, e che invece sia una quantità quantizzata, proprio come la lunghezza d'onda nella scatola. Sperimentalmente sappiamo che un oggetto incandescente splende di luce tanto più bluastra quanto più è caldo, e quindi è abbastanza naturale supporre che se l'energia è quantizzata, la quantizzazione sia proporzionale alla frequenza. In altri termini, noi adesso supponiamo che ciascuno degli "oscillatori elettromagnetici” che compare nella somma che dà l'energia totale non possa avere energie arbitrarie, ma solo multipli della frequenza.

Fu Max Planck, nel 1900, che fece la coraggiosa ipotesi di quantizzazione dell'energia, ipotesi che modifica radicalmente il teorema di equipartizione, e che risolve il problema della divergenza ultravioletta. 

Assumendo il nuovo valore per l'energia media, si ottiene una densità di energia elettromagnetica che non diverge più per frequenze molto alte.

Ref: https://wwwusers.ts.infn.it/~milotti/Didattica/LabTermodinamica/Blackbody.pdf